1億人のための統計解析をpythonで - case1_part1

1億人のための統計解析をpythonで - case1_part1

詳しい内容は書籍「西内啓『1億人のための統計解析』」をご参照ください。

解析案件整理

解析要件定義

要件	定義
アウトカム	過去3か月間における夜間帯の総利用金額
解析単位	顧客
説明変数	アウトカム以外のすべての項目

解析前の準備

データを読み込み総利用金額の列を追加します。

CODE

import scipy
import pandas as pd
import numpy as np
from statsmodels.stats.weightstats import ttest_ind
import matplotlib.pyplot as plt

# matplotlib日本語文字化け対策
# plt.rcParams['font.family'] = 'sans-serif'
# plt.rcParams['font.sans-serif'] = ['Hiragino Maru Gothic Pro', 'Yu Gothic', 'Meirio', 'Takao', 'IPAexGothic', 'IPAPGothic', 'VL PGothic', 'Noto Sans CJK JP']

# matplotlib日本語文字化け対策（colaboratory向け）
# !pip install japanize-matplotlib
# import japanize_matplotlib

plt.rcParams['font.size'] = 14

CODE

# ファイル読み込み
df = pd.read_excel('[ファイル設置パス]/case1.xlsx')

df['総利用金額'] = df['来店回数'] * df['利用金額']

Analysis 1: 顧客の性別や家族構成は売り上げに影響を与えるか

総利用金額の違いが男女によって生じるかどうかを検証する

男性・女性それぞれの平均総利用金額を算出する

CODE

dfa = df.groupby('性別').mean()
print(
  f"女性の平均総利用金額: {dfa.loc['女性']['総利用金額']}",
  f"男性の平均総利用金額: {dfa.loc['男性']['総利用金額']}",
  f"[女性]と[男性]の平均総利用金額の差: {dfa.loc['女性']['総利用金額'] - dfa.loc['男性']['総利用金額']}",
  sep='\n'
  )

OUTPUT

女性の平均総利用金額: 1322.9755178907722
男性の平均総利用金額: 2384.4349680170576
[女性]と[男性]の平均総利用金額の差: -1061.4594501262854

女性を基準に算出しているので、女性の方が総利用金額が1000円ほど少ないという結果となります。

この差は偶然起きるものなのか検定する

2つの母集団における差が偶然かどうかを検証する手法としてウェルチのt検定というものがあります。対象の母分散が等しくない（非等分散）ときに使う手法でありますが

母分散が未知の時に適用したときの影響
等分散検定を行った場合による、検定の多重性の影響

これらを考慮していれば、母分散に関する情報がなくても利用することも考えられます。ここではそのまま利用する方針をとるとして

CODE

# ウェルチのt検定を実施
samplea = df[df['性別']=='女性']['総利用金額']
sampleb = df[df['性別']=='男性']['総利用金額']
t, p, dof = ttest_ind(samplea, sampleb, usevar='unequal')

print(
    f"自由度: {dof}",
    f"t値: {t}",
    f"p値: {p}",
    sep='\n'
    )

OUTPUT

自由度: 849.4363751215236
t値: -3.4347473789710277
p値: 0.000621842190808965

結果の読み取り

p値が0.0006強と算出されました。これは確率0.06%でこの差が得られるということを示しています。つまりたまたまこのような結果が得られる可能性は限りなく少なく、めずらしいことが起きているということです。

なお1000回に1回しか起きない事象の発生確率は0.1%で数量に置き換えると0.001となりますが、今回のp値の結果『0.0006強』を小数点第3位までを用いて<0.001と表すことが慣習としてあるようです。これは小数点第3位までとして0.000と表現してしまうと、確率が0であると示していることになり、正確性が損なわれます。実際は0.0006強であり、0ではないことを示す表現である方が正確であるということです。

またこのp値という値はイメージで理解する方が容易であると考えられ、下記のように確率密度関数によるグラフをイメージすると良いです。

# t分布の描画
fig, (ax, ax2) = plt.subplots(1, 2, figsize=(12,6))

# 左側の図表
ax.set_title(f"自由度{dof:.0f}のt分布")
ax.set_ylabel('y')
ax.set_xlabel('x')
ax.grid(True)

x1 = np.linspace(-4, 4, 100)
y1 = scipy.stats.t.pdf(x1, dof)

ax.plot(x1, y1)

ax.annotate(f"{t:.3f}", xy=(t, scipy.stats.t.pdf(t, dof)),
            xytext=(-4,0.1),
            arrowprops=dict(width=1, facecolor='black'),
            )


# 右側の図表
ax2.set_title('左の図表の一部を拡大したもの')
ax2.set_ylabel('y')
ax2.set_xlabel('x')

x2 = np.linspace(-4, -3, 100)
y2 = scipy.stats.t.pdf(x2, dof)
ax2.plot(x2, y2)

ax2.annotate(f"{t:.3f}", xy=(t, scipy.stats.t.pdf(t, dof)),
            xytext=(-3.8, 0.003),
            arrowprops=dict(width=1, facecolor='black'),
            )

fill_x = np.linspace(-4, t, 25)
fill_y = scipy.stats.t.pdf(fill_x, dof)
ax2.fill_between(fill_x, fill_y, facecolor='cyan', alpha=0.3)

OUTPUT

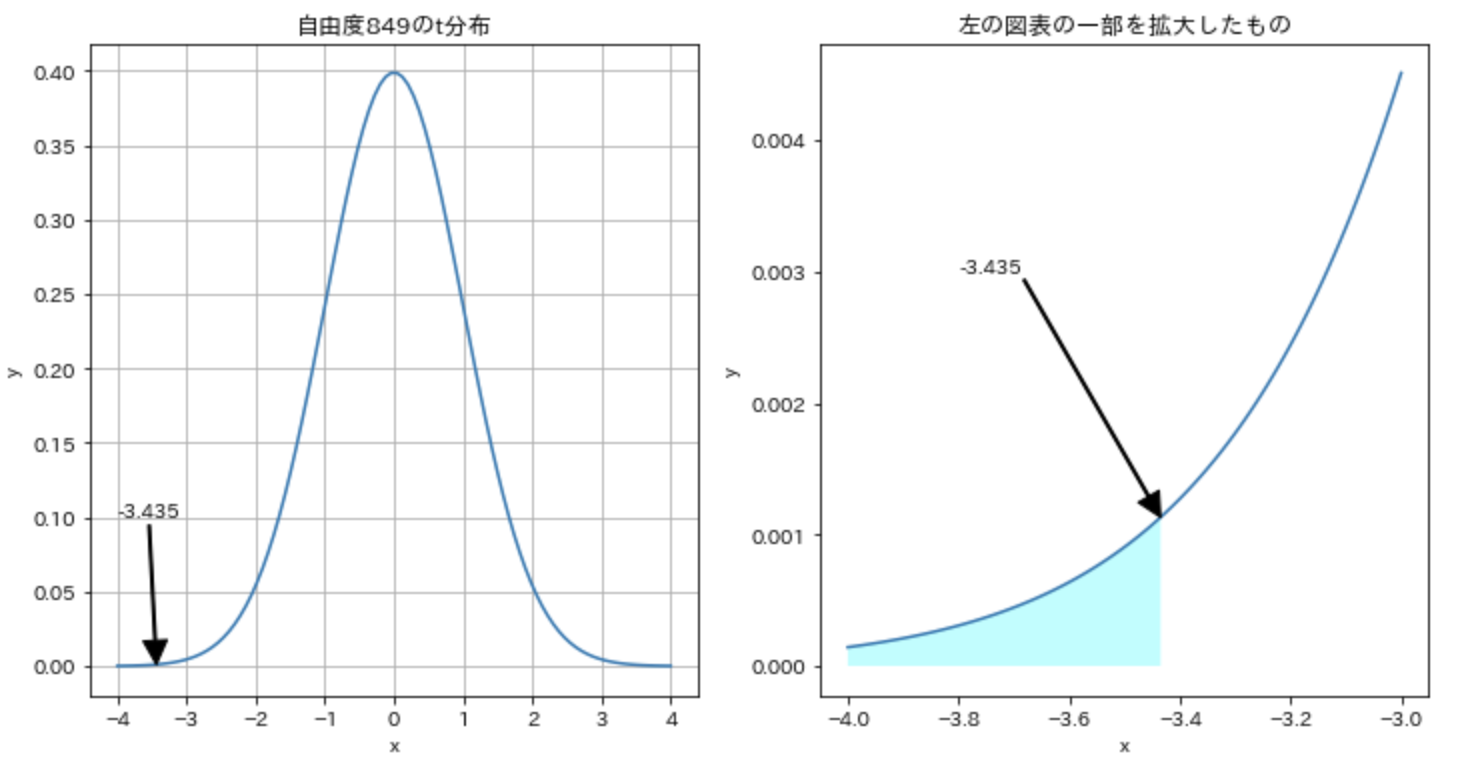
CODE

# 累積分布関数（cumulative distribution function）
print(f"累積分布関数よりt値 {t:.3f} までの面積は {scipy.stats.t.cdf(t, dof)} となります。")

print(f"一方、p値は {p} となっており、一致していませんが、これは両側確率です。")

print(f"したがってt値より得られた片側確率の面積を2倍すれば {scipy.stats.t.cdf(t, dof) * 2} となり一致します。")

OUTPUT

累積分布関数よりt値 -3.435 までの面積は 0.0003109210954044825 となります。
一方、p値は 0.000621842190808965 となっており、一致していませんが、これは両側確率です。
したがってt値より得られた片側確率の面積を2倍すれば 0.000621842190808965 となり一致します。

総利用金額の違いが家族構成によって生じるかどうかを検証する

家族構成は

結婚していない
結婚している（子供あり）
結婚している（子供なし）

の3つの状態をとる説明変数。ウェルチのt検定による先ほどの比較手法は異なる2つの母集団における手法であり、3つの集団には適用できません。この場合の解決策の例は

基準グループを決め、基準に対する比較を繰り返す
結婚している・していないに分類し直し集団の数を2つに抑える

などがあります。ここでは基準グループを決め比較を繰り返すかたちで検定します。

平均総利用金額の算出

各集団それぞれにおける総利用金額の平均は

CODE

samplea = df[df['家族構成']=='結婚していない']['総利用金額']
sampleb = df[df['家族構成']=='結婚している(子供あり)']['総利用金額']
samplec = df[df['家族構成']=='結婚している(子供なし)']['総利用金額']

print(
  f"結婚していないの平均総利用金額: {samplea.mean()}",
  f"結婚している(子供あり)の平均総利用金額: {sampleb.mean()}",
  f"結婚している(子供なし)の平均総利用金額: {samplec.mean()}",
  sep='\n'
  )

OUTPUT

結婚していないの平均総利用金額: 1476.2820512820513
結婚している(子供あり)の平均総利用金額: 2206.1032863849764
結婚している(子供なし)の平均総利用金額: 1793.3962264150944

今回は子供ありの集団が一番多いという結果が得られました。

これらの差が偶然発生するものかどうかを検証する

つづいて、この差が偶然によるものかどうかを検証します。

CODE

print(
  f"# [結婚していない]と[結婚している(子供あり)]",
  f"平均総利用金額の差: {samplea.mean() - sampleb.mean()}",
  sep='\n'
  )

t, p, dof = ttest_ind(samplea, sampleb, usevar='unequal')
print(
    f"自由度: {dof}",
    f"t値: {t}",
    f"p値: {p}",
    sep='\n'
    )

print('')

print(
  f"# [結婚していない]と[結婚している(子供なし)]",
  f"平均総利用金額の差: {samplea.mean() - samplec.mean()}",
  sep='\n'
  )

t, p, dof = ttest_ind(samplea, samplec, usevar='unequal')
print(
    f"自由度: {dof}",
    f"t値: {t}",
    f"p値: {p}",
    sep='\n'
    )

OUTPUT

# [結婚していない]と[結婚している(子供あり)]
平均総利用金額の差: -1061.4594501262854
自由度: 849.4363751215236
t値: -3.4347473789710277
p値: 0.000621842190808965

# [結婚していない]と[結婚している(子供なし)]
平均総利用金額の差: -470.4207085243222
自由度: 152.5549433878091
t値: -1.1183507093164164
p値: 0.2651751873825952

結果の読み取り

p値に着目すると下表のように整理できます。

比較対照	基準に対する平均総利用金額の差	p値	偶発的に得られるか
[結婚していない]と[結婚している(子供あり)]	-729	0.028	x
[結婚していない]と[結婚している(子供なし)]	-317	0.460	o

したがって、結婚していない顧客より

子供がいる既婚者の顧客は700円強消費が多く、偶然の結果ではないことが分かる
子供がいない既婚者の顧客は300円強消費が多いという算出結果だが、これは偶発的に得られた可能性がある

ということが分かりました。

続く・・・

参考文献

西内啓『1億人のための統計解析』
西内啓『統計学が最強の学問である[実践編]』